重要性采样、NEE和MIS
上一节中,我们构建了一个基础直白的路径追踪框架,使用半球均匀采样,而且直到光线随机碰巧撞上光源,才结束碰撞,这样很好理解,但是收敛速度很慢。接下来两节中,尝试结合多种采样改进技术,旨在减少方差、提高每个样本的贡献效率,从而在相同采样次数下获得更接近真实解的图像
轮盘赌中止
Russian Roulette(俄罗斯轮盘赌)本身就是一种加速收敛速度的技术,光线多次反弹后,携带的能量比较低,贡献也比较弱,因此直接舍弃可以一定程度控制平均路径长度、减少无意义计算,上一节中已经包含了这个方法:
if (bounce > 2) {
float p = max(throughput.r, max(throughput.g, throughput.b)); // 生存概率,亮度越低越容易被中止
if (rng_nextFloat(rng) > p) break; // 有概率终止路径
throughput /= p; // 补偿被采样概率
}
也可以看出,各种提升收敛速度方法的核心,在于选择一个“更有意义”的分布进行采样,然后用该分布的 概率密度函数(PDF)去归一化补偿,从而保持无偏性。轮盘赌中止基本可以看作此方法的最简单实践
重要性采样
核心思路还是不变,更具体的解释在上一节光线采样部分提过了。对于Cook-Torrance BRDF,GGX 法线分布函数(NDF)上的重要性采样函数是比较常见的:
vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
float a = roughness\*roughness;
// 采样方向的极坐标参数化
float phi = 2.0 * PI * Xi.x;
float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
float sinTheta = sqrt(1.0 - cosTheta*cosTheta);
// 局部坐标系下构建半程向量 H
vec3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
// 切线空间 → 世界空间转换
vec3 up = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
vec3 tangent = normalize(cross(up, N));
vec3 bitangent = cross(N, tangent);
vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
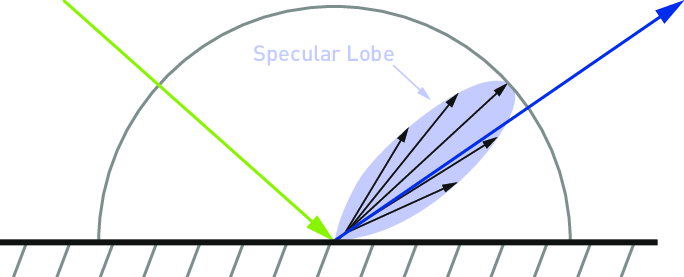
基本上就是集中在上图的紫色区域中采样,粗糙度越大,紫色扩散范围越大,替换之前的均匀半球采样:
vec2 Xi = sobol2D(samples, bounce, rng.state);
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
vec3 L = normalize(reflect(-V, H)); // 重要性采样生成 H,再反射得 L
接下来是重点,这里要用到的L的概率分布,计算起来没有那么容易,后面的内容选择性观看即可:
先给完整的结果:
GGX 的法线分布函数(NDF)是:
ImportanceSampleGGX 的采样是在半程向量空间
把 PDF 从 H 映射到 L:
我们最终用的是出射方向
反射关系中
从
映射到 时的 Jacobian determinant 为:
最终重要性采样在 L 方向上的 PDF 是:
这上面的两步都是某种换元方法,没有这些,将无法保证能量的守恒。积分时的换元在后面的各种操作中非常常见,下面顺带讲解一下
测度转换
这一步困惑了我挺久的,主要原因是
| 概念 | 符号 | 单位 | 描述 |
|---|---|---|---|
| 辐射通量(Radiant Flux) | W | 每秒发出的总能量 | |
| 辐照度(Irradiance) | W/m² | 单位面积上接收到的通量 | |
| 辐射亮度(Radiance) | W/(sr·m²) | 单位面积、单位立体角方向上的辐射能量密度 |
对于渲染方程:
对于Cook-Torrance BRDF :
除了
这里有两种方式来理解额外的项:
首先一个不太显然的事实是,
对于:float DistributionGGX(vec3 N, vec3 H, float roughness)
| roughness | ∫ D · cosθ dω (这个=1) | ∫ D dω (>1) |
|---|---|---|
| 0.1 | ≈ 1.08 | ≈ 1.08 |
| 0.3 | ≈ 0.99 | ≈ 1.01 |
| 0.5 | ≈ 1.00 | ≈ 1.13 |
| 0.8 | ≈ 1.00 | ≈ 1.54 |
| 1.0 | ≈ 1.00 | ≈ 2.00 |
提到这么多,主要是很多书籍/教程对这一点确实有不同选择,例如 https://pbr-book.org/4ed/contents 9.6 中是没有写这一项的,很多地方还混合两种定义来讲解,导致一开始理解比较混乱。现在只要接受了Cook-Torrance中的
其定义的值就是朝某个方向上的微表面面积,例如:
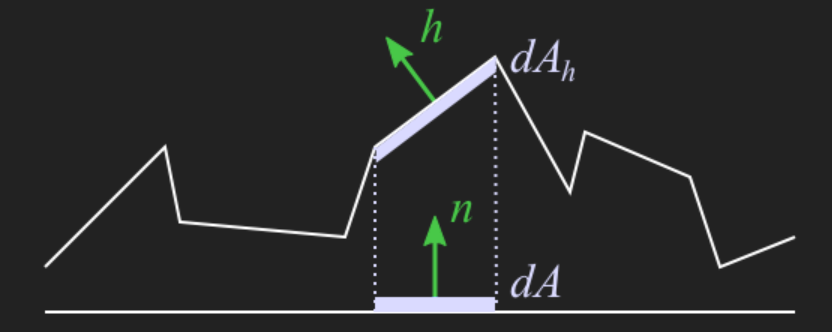
直观上来理解,这个斜着的微表面,明显从归一化的角度来讲,其面积有点”虚标“了,乘个
严谨一点,测度转换本质上就是积分时的变量替换,都可以用雅可比矩阵来解释,这里也以此为例子,顺便梳理一下:
雅可比矩阵
对于一个坐标映射
它的 Jacobian 是各分量对自变量的偏导排成的矩阵
det J(行列式)给出了一个局部“缩放率”:在微元尺度内
也就是从
-域到 -域的面积 / 体积 / n-维测度变化因子
测度转换(积分变量替换)
在积分里,这个缩放率就是 换元公式:
从面积域 dA 到方向角域 dω
可以都从 极角
方向角表达式
雅可比矩阵
面积伸缩因子(行列式)
把两列做叉乘即可得到在单位球面上的微元面积
于是有:
这个公式也是一般对于方向角定义的直观理解,就是一小块矩形的面积:
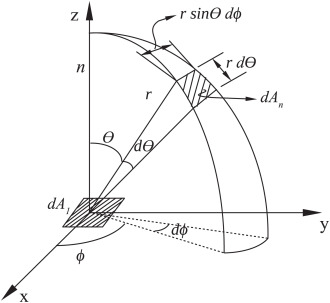
面积微元表达式
同样是上面的步骤,可得:
最后就可以看出:
所以对于
相似的内容在图形学中还挺常见的,例如 https://www.pbr-book.org/3ed-2018/contents 中的5.5章,提到了投影立体角与立体角,同样是一个cos的转换关系
从 H 映射到 L
上面讲解了测度转换后,求重要性采样PDF时,把 PDF 从 H 映射到 L 就是类似的操作了,这里不多赘述
混合采样
GGX重要性采样仅针对Cook-Torrance中的高光项,漫反射部分还是需要使用均匀半球采样,或者替换为余弦加权半球采样。如何混合两种不同的采样呢?有一个简单的方法,就是根据一个概率,例如0.5,那就是一半概率根据余弦加权半球采样,一半根据GGX重要性采样,然后平均这两个采样的PDF,代码如下:
float pdfSelSpec = 0.5;
float pdfSelDiffuse = 1.0 - pdfSelSpec;
// ---------------------------------------------------------------
vec2 Xi = sobol2D(samples, bounce, rng.state);
float rTech = rng_nextFloat(rng); // 随机数决定采样方法
vec3 L; // 采样出的入射方向
float pdfSpec = 0.0;
float pdfDiff = 0.0;
if (rTech < pdfSelSpec) // --- 镜面分支:GGX importance sample ---
{
vec3 H = ImportanceSampleGGX(Xi, N, roughness);
L = normalize(reflect(-V, H));
float NdotH = max(dot(N, H), 0.0);
float HdotV = max(dot(H, V), 0.0);
pdfSpec = DistributionGGX(N, H, roughness) * NdotH / (4.0 * HdotV + 1e-4);
pdfDiff = max(dot(N, L), 0.0) / PI; // 同时算出漫反射 pdf
}
else // --- 漫反射分支:余弦加权 ---
{
L = cosineSampleHemisphere(Xi, N);
pdfDiff = max(dot(N, L), 0.0) / PI;
vec3 H = normalize(V + L);
float NdotH = max(dot(N, H), 0.0);
float HdotV = max(dot(H, V), 0.0);
pdfSpec = DistributionGGX(N, H, roughness) * NdotH / (4.0 * HdotV + 1e-4); // 同时算出GGX 会是什么 pdf
}
在两个分支中,都计算两种PDF,后续根据概率平均这两种PDF即可。当然这个方法只是可行,本质上不会加快收敛的速度(降低方差),并且这个比值需要是较准确的,否则估计偏差会较大,这里选择0.5肯定只是临时方案,后面可以通过优化菲涅尔能量占比估计来解决,相关问题会在后面的MIS中讨论
直接灯光采样
直接灯光采样,也叫Next Event Estimation (NEE)(下一事件估计)是一种将直接光照项显式采样的技术,给个传送门:https://www.bilibili.com/video/BV1X7411F744/?spm_id_from=333.788.videopod.episodes&vd_source=fe7a9ee6657422d709d30bf6284f347f&p=16 大概1h左右开始有提到,视频里的图示很清晰了,其中的:
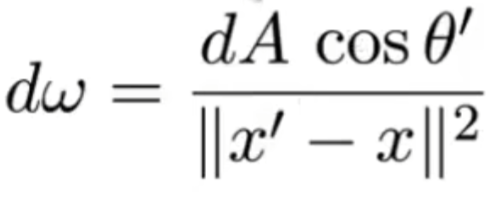
同样是一个测度转换,不过这个严谨推导就复杂很多了,Physically Based Rendering中也是一笔带过,所以就从几何直观上理解一下算了
NEE引入了新的采样分布,但和上面的漫反射/高光可以采用简单的混合采样方法不同,NEE需要额外打出一根光线,为了在这种情况下保持无偏,需要使用MIS
多重重要性采样(Multiple Importance Sampling)
上面提到了混合采样并不能本质的降低方差,提高收敛速度。其与MIS的区别在于,混合采样中,根据某个概率,选择一个分支,实际上每次bounce还是只采样打出了一根光线。而MIS则不同,每次bounce不是选择分支,而是实际打出多根光线,然后考虑如何加权。关于混合采样为什么无法降低方差,以及MIS理论,见:https://www.pbr-book.org/3ed-2018/contents 13.10章节,不过比较简略,MIS实际上对每根光线的采样分布以及其PDF有一些约束,不过目前不太需要考虑,这里先忽略,后续的章节可能会补全
其实前面的漫反射/镜面分支同样可以升级为MIS,但三次采样会比较复杂,暂时不弄了,仅以NEE说明如何使用MIS
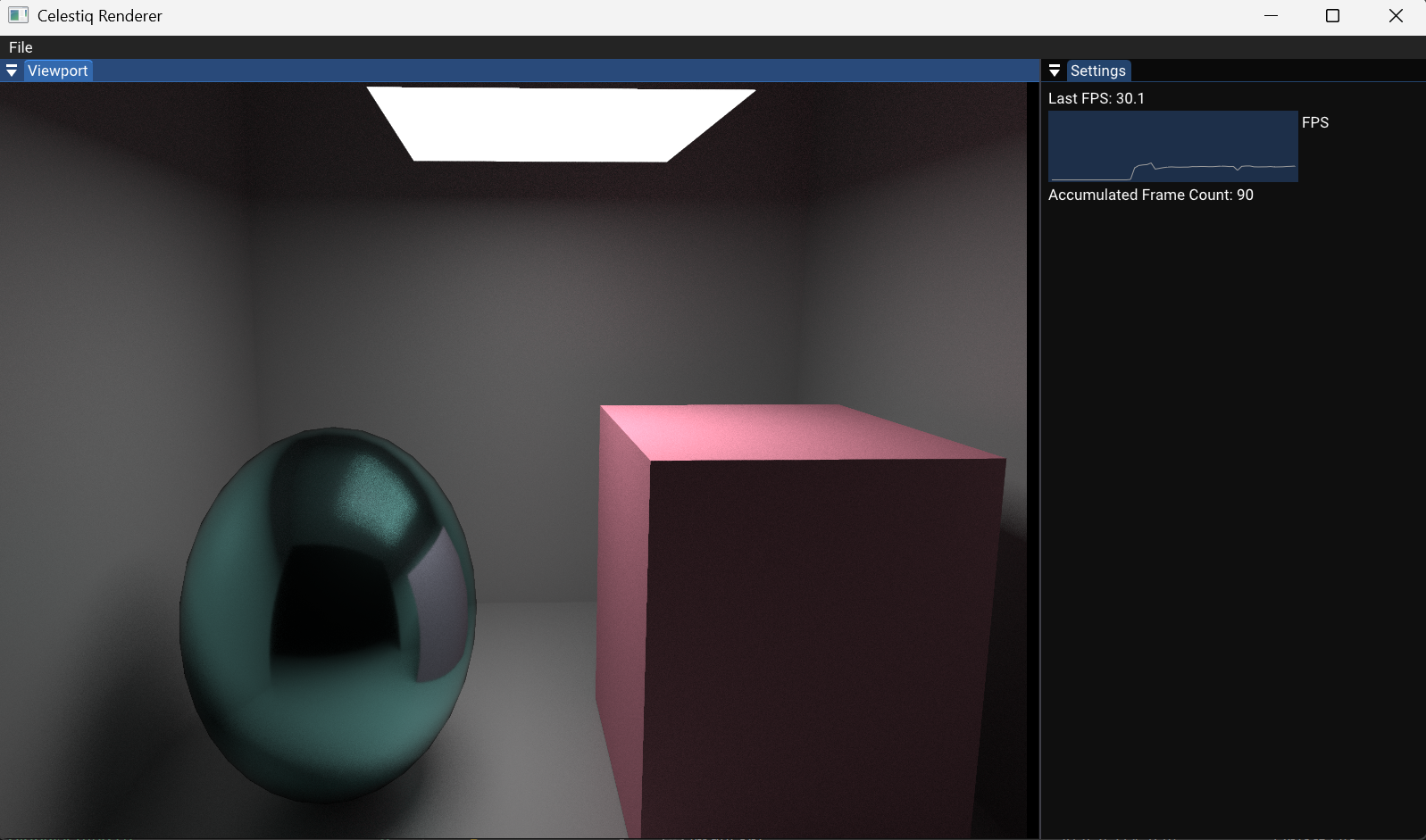
如果渲染时出现了"fireflies",即不合理的高亮像素,例如下图右上角,MIS策略有误可能是部分原因:

先为NEE添加几个函数,用于替代之前的光线求交:
float sampleLightIndex(inout RNGState rng);
LightSample sampleFaceLight(uint idx, vec2 Xi);
LightSample sampleDirectionalLight();
第一个用于从灯光power加权采样,为每个灯光添加cdf变量,记录其“面积 * 强度”作为其power,越强的灯光越容易被采样到,当然这个逻辑不是必须的,直接随机选一个灯光也是可以的
后面两个函数用于从灯光采样出如下信息:
struct LightSample {
vec3 pos; // 采样点世界座标
vec3 normal; // 面法线(已归一化)
vec3 radiance; // lightColor * intensity
float pdfArea; // 对 *面积* 的 pdf
int isDelta; // 方向光 = 1,面光 = 0
};
重点是面光源,需要从面中随机选点和计算其面积,详细的过程在函数当中,不详细展开了
接下来定义简化版的求交函数,仅用于检测某点的光源可见性,一旦检测出更近的物体就退出返回false:
bool traceShadow(vec3 rayOrig, vec3 rayDir, float maxDist, int rootIndex);
bool traceBLAS_shadow(int rootIndex, vec3 rayOrig, vec3 rayDir, mat4 model, float maxDist, int baseIndexOffset);
接下来,在主循环中,删除之前的灯光求交逻辑,开始采样灯光:
// 采样灯光
float selRand = rng_nextFloat(rng);
vec2 XiLight = sobol2D(samples*3u, bounce*7u, rng.state);
LightSample ls;
float pdfLight = 1.0;
if (selRand < 0.8 && faceLights.length() > 0) // 80 % 面光
{
uint idx = uint(sampleLightIndex(rng)); // 按功率 CDF 采样,更可能采样到强光源
ls = sampleFaceLight(idx, XiLight);
float seg = faceLights[idx].cdf - (idx==0?0.0:faceLights[idx-1].cdf);
pdfLight = seg * ls.pdfArea * 0.8; // 面积 pdf
}
else // 20 % 方向光
{
ls = sampleDirectionalLight();
pdfLight = 1.0 * 0.2; // δ pdf
}
这里的通过一个概率选择采样面光还是方向光,目前硬编码了一个概率,这是不对的,此概率最好按照渲染处面光和方向光的真实能量比来选择(这不可能,但按整个场景的面光和方向光能量比来选择也是不错的),后面再优化。这样就得到了第一根光线L1,然后计算一些所需的变量:
vec3 L1 = (ls.isDelta==1) ? -normalize(ls.normal)
: (ls.pos - hitInfo.hitPos);
float distLight = length(L1);
L1 /= distLight;
float NdotL1 = dot(N, L1);
float L1Ndot = (ls.isDelta==1) ? 1.0
: max(dot(ls.normal, -L1), 0.0);
检测一下合法性,省略的部分就是重点:
if (NdotL1 > 0.0 && L1Ndot > 0.0)
{
// 检测光源可见性
bool blocked = traceShadow(hitInfo.hitPos + N*1e-4,
L1, distLight-2e-4, tlasRoot);
if (!blocked)
{
// ......
}
}
radiance += direct; // ← 立即累加直接光
首先是积分域转换,公式和上面图中一致:
// 面光 pdf 转 solid-angle
if (ls.isDelta == 0)
pdfLight *= (distLight*distLight) / L1Ndot;
pdfLight = max(pdfLight, 1e-4);
然后计算BRDF,这个和之前一样,就不贴了。重点是计算MIS权重,如果觉得Physically Based Rendering中公式不太清晰,贴一个更清晰的版本:
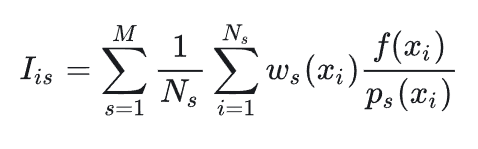
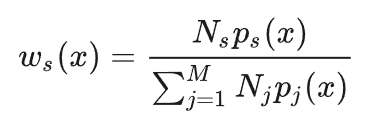
其中的
// 计算混合采样pdf
float pdfSpec = DistributionGGX(N,H,roughness)
* max(dot(N,H),0.0)
/ (4.0*max(dot(H,V),1e-4));
float pdfDiff = NdotL1 / PI;
float pdfSelSpec = max(max(kS.r, kS.g)b); // 此策略和下方需保持一致
float pdfSelDiffuse = 1.0 - pdfSelSpec;
float pdfBsdf = pdfSelSpec * pdfSpec + pdfSelDif* pdfDiff;
pdfBsdf = max(pdfBsdf, 1e-4);
// 计算MIS 权重
float w = (pdfLight*pdfLight) /
(pdfLight*pdfLight + pdfBsdf*pdfBsdf);
注意在计算混合采样pdf时,需要采用和上文中提到的混合采样一致的策略
最后根据公式更新直接光源采样项:
direct = throughput * f_brdf * ls.radiance * NdotL1 * w / pdfLight;
后面接上混合采样步骤,采样第二根光线即可,这里就不贴了,有一个重点,在混合采样阶段,依旧是需要按照上面的原理,计算直接光照采样的PDF,计算MIS权重。但注意:pdfLight本质上是采样点采样到光源的概率,所以和光线方向没关系,并不需要重新计算这个值(这一段有误,见下面的更正):
// 计算 MIS 权重
float w_bsdf = (pdfCombined * pdfCombined) /
(pdfCombined * pdfCombined + pdfLight * pdfLight);
最后一件事:
// 常量:防止粗糙度为0
const float MIN_ROUGHNESS = 0.05;
float roughness = max(mat.roughness, MIN_ROUGHNESS);
粗糙度不能太小,会导致DistributionGGX()函数给出过大值,然后计算MIS权重时还平方了一下,直接导致数值溢出,想要完全解决这个问题,需要再添加一条采样分支,当粗糙度很小时,替换DistributionGGX()采样方法为完全反射。低粗糙度是个很棘手的问题,后续很多算法都需要将极小粗糙度单独处理,目前就优化视觉效果提升不大,我这里就先不做了
构建
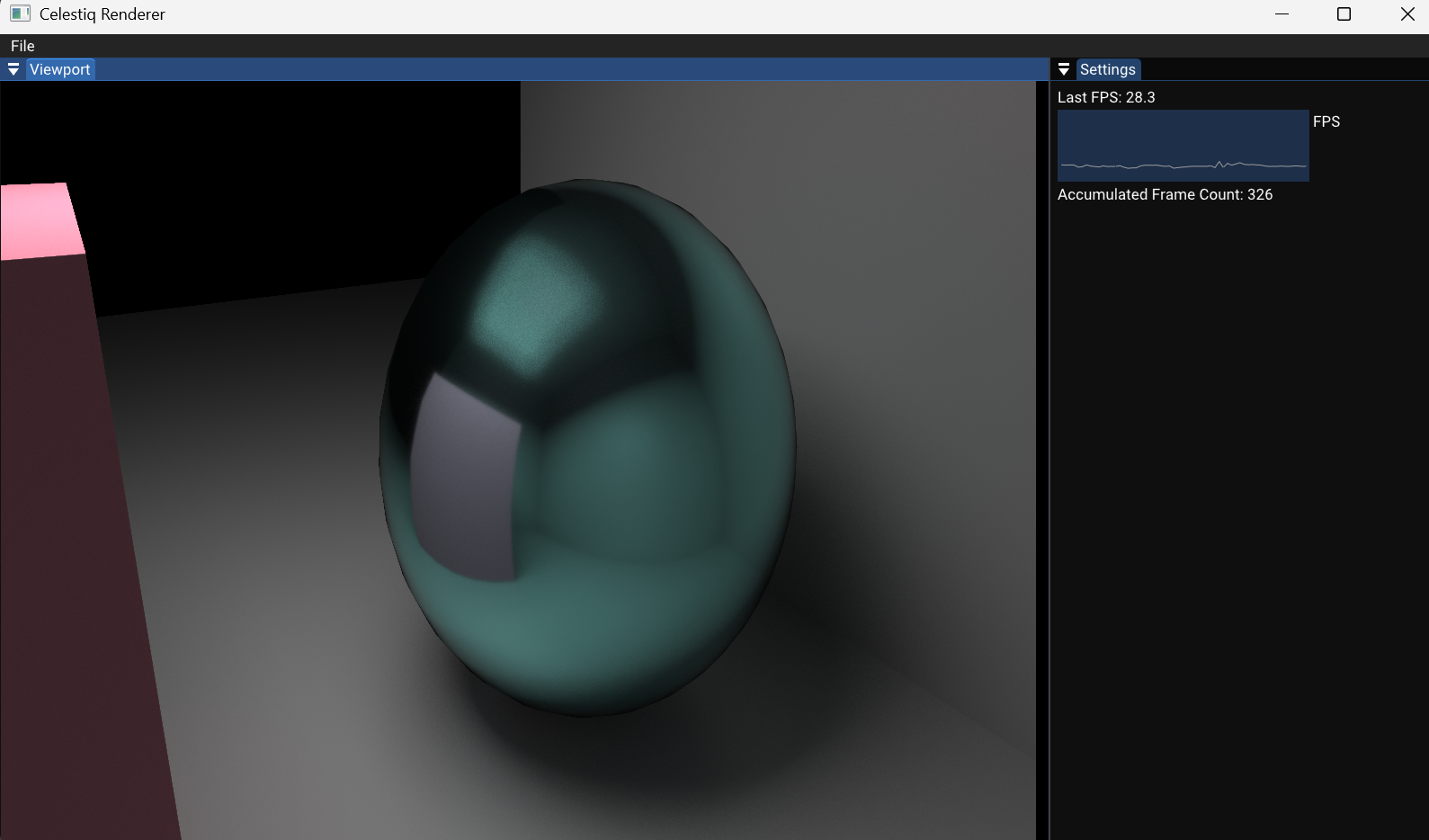
这一章内容确实挺多,不过结果是值得的,把球换上了最低粗糙度的材质,可以看到,镜面反射效果不错,而且背景拐角处的环境光遮蔽的感觉也明显了很多,整体噪点也变少了
采样效率较上一节最基础的均匀半球采样,可能提升了大概50-100倍,由于采样效率整一个大提升,我这边降低参数到MAX_BOUNCES = 4,SAMPLES_PER_PIXEL = 2,可以换取一些帧数,从4帧提升至电竞帧率30帧(甚至还提高了一些球体的细分数),但依旧能在1秒以内就收敛到一个不错的画面
关于MIS权重的误解
这一段是后补上的,上面关于MIS的权重计算存在一些错误,关键在于:NEE和BSDF sampling最终对于光线权重的处理:
// NEE
direct = throughput * f_brdf * ls.radiance * NdotL1 * w / pdfLight;
radiance += direct;
// BSDF sampling
throughput *= f_bsdf * NdotL2 * misW / pdfCombined;
我这里错误的将MIS权重理解为一种能量分配,也就是这一次反弹选择的两条光线的能量比重,实际上是不对的
对于NEE,将其结果直接累积到了radiance中,意味着这条光线结束了,真正完成了一次“采样”,计算了最终的积分。而对于BSDF sampling,只是计算了throughput,并继续下一跳,光线并没有结束
所以上文对于“采样”一词表述并不准确,实际上,在计算BSDF sampling时,只是反弹了光线,没有完成一次采样。区分此的关键就是有没有真正累积radiance变量,这个变量才是真正的积分结果
因此MIS权重的计算错误就很清晰了,第一:只有当真正的采样结束时,才需要乘上MIS权重,因此NEE部分的代码是正确的,BSDF sampling中:throughput *= f_bsdf * NdotL2 / pdfCombined; 删掉misW即可。第二:何时考虑BSDF sampling的MIS权重呢?答案是不需要,我这里由于NEE效果太好,直接删除了BSDF sampling碰巧撞上光源的采样方法,因此实际上所有的光路都来自NEE
按道理来说BSDF sampling碰巧撞上光源的采样路线也是有必要的,下图展示了两种采样方法的优劣: 
NEE对于低粗糙度物体+大光源采样效率比较低,我后面仔细观察金属球上的面光反光,发现收敛速度确实偏慢,不过不是很明显,所以忽略了这一点:

如果加上BSDF sampling碰巧撞上光源的采样路线的话,那么如何计算此时的MIS权重呢?首先需要记录下NEE采样的哪个光源,例如光源A,在下一次弹跳中,若光源碰巧撞上了光源A,那么按照上文的方法计算MIS权重。其他情况例如光线击中了光源B(或其他物体),那么pdfLight即采样A光源的函数采样此时的光线的概率是多少?采样A光源的函数不可能采样到B光源,所以为0,MIS权重为1
其实MIS权重要做到完全数学正确,还有非常多优化空间,例如其实光线的每一跳都执行了一次NEE采样,最后执行一次BSDF sampling碰巧撞上光源的采样结束,这样完全按照MIS权重的公式来的话,会非常麻烦,实际开发中,忽略所有碰巧撞上光源的采样策略的MIS权重,是没有问题的
代码存档
代码下载